古典コンピュータを使った量子化学計算を実行してみる

[2]:

!pip install pyscf
!pip install matplotlib

Found existing installation: h5py 3.4.0
Uninstalling h5py-3.4.0:
  Would remove:
    /usr/local/lib/python3.9/site-packages/h5py-3.4.0.dist-info/*
    /usr/local/lib/python3.9/site-packages/h5py/*
Proceed (y/n)?   Successfully uninstalled h5py-3.4.0
Requirement already satisfied: pyscf in /usr/local/lib/python3.9/site-packages (1.7.6)
Collecting h5py>2.2
  Using cached h5py-3.4.0-cp39-cp39-macosx_10_9_x86_64.whl (3.0 MB)
Requirement already satisfied: numpy!=1.16,!=1.17,>1.8 in /usr/local/lib/python3.9/site-packages (from pyscf) (1.20.3)
Requirement already satisfied: scipy!=1.5.0,!=1.5.1 in /usr/local/lib/python3.9/site-packages (from pyscf) (1.6.3)
Installing collected packages: h5py
Successfully installed h5py-3.4.0
WARNING: You are using pip version 21.1.3; however, version 21.2.4 is available.
You should consider upgrading via the '/usr/local/opt/python@3.9/bin/python3.9 -m pip install --upgrade pip' command.
Requirement already satisfied: matplotlib in /Users/yuichiro/Library/Python/3.9/lib/python/site-packages (3.4.1)
Requirement already satisfied: kiwisolver>=1.0.1 in /Users/yuichiro/Library/Python/3.9/lib/python/site-packages (from matplotlib) (1.3.1)
Requirement already satisfied: python-dateutil>=2.7 in /Users/yuichiro/Library/Python/3.9/lib/python/site-packages (from matplotlib) (2.8.1)
Requirement already satisfied: pillow>=6.2.0 in /Users/yuichiro/Library/Python/3.9/lib/python/site-packages (from matplotlib) (8.2.0)
Requirement already satisfied: pyparsing>=2.2.1 in /Users/yuichiro/Library/Python/3.9/lib/python/site-packages (from matplotlib) (2.4.7)
Requirement already satisfied: cycler>=0.10 in /Users/yuichiro/Library/Python/3.9/lib/python/site-packages (from matplotlib) (0.10.0)
Requirement already satisfied: numpy>=1.16 in /usr/local/lib/python3.9/site-packages (from matplotlib) (1.20.3)
Requirement already satisfied: six in /Users/yuichiro/Library/Python/3.9/lib/python/site-packages (from cycler>=0.10->matplotlib) (1.15.0)
WARNING: You are using pip version 21.1.3; however, version 21.2.4 is available.
You should consider upgrading via the '/usr/local/opt/python@3.9/bin/python3.9 -m pip install --upgrade pip' command.

[3]:

import numpy as np
import matplotlib.pyplot as plt
from pyscf import gto, scf
from pyscf import fci
from pyscf import cc, mp, dft

古典コンピュータを使った量子化学計算を実行してみる#

本勉強会の受講者には、量子化学計算に馴染みがない方も多いと思います。 そこで、まずは、「従来型」の量子化学計算に触れていただきます。

水素分子の計算（平均場近似と厳密対角化）#

ここでは、最も単純な分子である、水素分子(\(H_2\))の基底状態を求めてみます。 ソフトウェアには、PySCFというプログラムを用います。 計算方法は、平均場近似（Hartree-Fock)法と、厳密対角化（化学ではFull CIという）をそれぞれ実行してみます。

また、通常の量子化学計算では、有限個のGauss型原子基底関数の線形結合で１電子波動関数（軌道）を記述します (Linear combination of atomic orbitals method, LCAO)。

\[\psi_i(r) = \sum_{p} C_{ip}\xi_p(r)\]

この有限個の原子基底関数は、既に標準的に使われているものがいくつもあります。 今回は、その中でも最も単純な、STO-3Gという基底関数を使います。 STO-3Gでは、各水素原子にはそれぞれ１つのｓ型の軌道が使われています。 水素分子としては、２つの「空間」軌道があることになります。

\[\xi_{1s}(r) = \sum_{i=1}^3 d_{i,1s}g_{1s}(a_i,r)\]

さて、電子にはスピンの自由度があるので、↑と↓のスピンの自由度ごとに空間軌道に電子が入ります。 スピンの自由度ごとに入る軌道をスピン軌道といいます。

\[\begin{split}\chi(x) = \begin{cases} \psi(r)\alpha(\omega) \\ \textrm{or} \\ \psi(r)\beta(\omega) \end{cases}\end{split}\]

スピン軌道は空間軌道の２倍の数があります。STO-3G基底関数を使った場合、 水素分子には4つのスピン軌道があることになります。 水素には電子が２つあるので、電子があるスピンに存在する場合を１、しない場合を０としましょう。 すると、電子の詰まり方（電子配置は）、0011, 0101, 1001, 1100, 1010, 0110 の6パターンが存在することがわかります。

平均場近似では、電子の波動関数は一つのSlater行列式（一つの電子配置）であらわされます。 つまり、先程の６パターンうち１つの電子配置しか取らないと仮定して（例えば、0011)、 その仮定のもとでエネルギーが最小化される軌道を見つけます。

厳密対角化（Full CI)では、全ての取りうる電子配置を考えて、その重ね合わせで、 波動関数を表現します。

\[|\Phi_{\textrm{CI}}\rangle = c_{0011}|\Psi_{0011}\rangle + c_{0101}|\Psi_{0101}\rangle + c_{1001}|\Psi_{1001}\rangle + c_{1100}|\Psi_{1100}\rangle + c_{1010}|\Psi_{1010}\rangle + c_{0110}|\Psi_{0110}\rangle\]

今回の例では電子配置の数は少ないですが、電子配置の数は組み合わせ爆発をおこしますので、 計算コストは指数関数的に増大します。

さて、まず平均場（Hartree-Fock）計算を実行してみましょう。

[9]:

# 水素分子、H-H距離は0.74Å と設定。STO-3GというGaussian型の原子基底関数を使用。
# 3次元座標が(0, 0, 0)のHと、(0, 0, 0.74)のHを利用。
mol_h2 = gto.M(atom = 'H 0 0 0; H 0 0 0.74', basis = 'sto-3g')
# この水素分子の基底状態を平均場近似（Hartree-Fock theory)で計算してみる。
mean_filed_wavefunction = scf.RHF(mol_h2)
mean_filed_wavefunction.verbose = 0
hf_energy = mean_filed_wavefunction.kernel()
print ("Hartree-Fock Energy in (hartree)", hf_energy)

Hartree-Fock Energy in (hartree) -1.1167593073964248

次に、厳密対角化（Full CI)の計算をおこないます。

[10]:

full_ci_wavefunciton = fci.FCI(mean_filed_wavefunction)
fci_energy, fci_eigenvector = full_ci_wavefunciton.kernel()
print ("Full CI Energy (in hartree)", fci_energy)
print ("Hartree Fock/Full CI Energy (in %)", hf_energy/fci_energy*100)

Full CI Energy (in hartree) -1.1372838344885023
Hartree Fock/Full CI Energy (in %) 98.19530301322638

電子相関と電子相関エネルギー#

与えられたハミルトニアンに対する厳密解（Full CI)と平均場で解いたときのエネルギー（Hartree-Fockエネルギー）は、非常に近いことがわかる。平均場という単純な近似で、Full CIエネルギーの98.2%を再現している。一般におおよそ、Hartree-Fockは、全エネルギーの約99%を再現できると言われている。残りの約1%を電子相関エネルギーと呼ぶ。

この電子相関エネルギー(Electron Correlation Energy)を見てみよう。

[11]:

electron_correlation_energy = fci_energy - hf_energy
print ("Electron Correlation Energy in (hartree)", electron_correlation_energy)
print ("Electron Correlation Energy in (eV)", electron_correlation_energy*27.2114)
print ("Electron Correlation Energy in (kcal/mol)", electron_correlation_energy*23.0605*27.2114)

Electron Correlation Energy in (hartree) -0.020524527092077527
Electron Correlation Energy in (eV) -0.5585011165133584
Electron Correlation Energy in (kcal/mol) -12.879314997356303

電子相関エネルギーと化学的精度#

電子相関は、約0.56eV（13 kcal/mol)となっている。 さて、熱エネルギー（ボルツマン因子の逆数 \(1/\beta = k_bT\); \(k_b\)はボルツマン定数）は、室温298.15Kで約0.026eV (0.59kcal/mol)である。 熱エネルギーと比べると、電子相関のエネルギーは非常に大きい値であることがわかる。

分子の安定性（存在比）や、化学反応速度は、状態間のエネルギー差を\(\Delta E\)とするとボルツマン分布\(e^{-\beta \Delta E}\)に比例し、エネルギー差に対して指数的に減少（増大）する。 +/- 0.56eV (13kcal/mol)ほど、\(\Delta E\)に誤差があるとすれば、正解となる反応速度を１としたときに、誤差に応じて以下のように大きく変動する。

[12]:

print ("誤差が 0.56eVあったときの反応速度 %1.1e" %np.exp(-0.56/0.026))
print ("誤差が-0.56eVあったときの反応速度 %1.1e" %np.exp(0.56/0.026))

誤差が 0.56eVあったときの反応速度 4.4e-10
誤差が-0.56eVあったときの反応速度 2.3e+09

さて、誤差が 1kca/mol (約0.043eV)以下であった場合はどうだろう？

[13]:

print ("誤差が1kcal/mol(0.043eV)あったときの反応速度 %1.1e" %np.exp(-0.043/0.026))
print ("誤差が1kcal/mol(-0.043V)あったときの反応速度 %1.1e" %np.exp(0.043/0.026))

誤差が1kcal/mol(0.043eV)あったときの反応速度 1.9e-01
誤差が1kcal/mol(-0.043V)あったときの反応速度 5.2e+00

反応速度は、室温の場合、おおよそオーダーではあうことがわかる。 少なくとも、「反応速度（や存在比）のオーダーは予測できること」＝「化学における定量的計算」とするならば、量子化学の計算において目指すべき誤差はこの「1kcal/mol」となることがわかる。

代表的なその他の量子化学計算手法#

さて、では、計算の定量性を増すにはどうすればいいのだろうか？ 厳密にハミルトニアンを解く方法 Full CIは指数関数的な計算コストが必要となる。 このコストを下げるために、量子化学では、様々な近似理論が開発されてきた。 ここでは、計算コストが\(O(N^5)\)の二次の摂動論MP2、 現在の量子化学の「Golden standard」と称される\(O(N^7)\)の CCSD(T)、 そして、計算コストが\(O(N^3)\)で業界標準の方法となっているDFTという3つの手法を、 厳密な方法(Full CI)と比較してみよう。

水素分子は簡単過ぎるので、\(H_4\)という系を考えてみる。

[14]:

%%capture
hf_energies = []
mp2_energies = []
ccsdt_energies = []
fci_energies = []
dft_energies = []
r_list = []
for i in range(15):
  # H4、H-H距離を変化。STO-3GというGaussian型の原子基底関数を使用。
  r=0.5+i*0.15
  mol_h4 = gto.M(atom = 'H 0 0 0; H 0 0 %f; H 0 0 %f; H 0 0 %f' %(r,r*2,r*3),
  basis = 'sto-3g')
  # この水素分子の基底状態を平均場近似（Hartree-Fock theory)で計算してみる。
  mean_filed_wavefunction = scf.RHF(mol_h4)
  mean_filed_wavefunction.verbose = 0
  hf_energy = mean_filed_wavefunction.kernel()
  dft_wavefunction = dft.RKS(mol_h4)
  dft_wavefunction.verbose = 0
  dft_wavefunction.xc = 'B3LYP'
  dft_energy = dft_wavefunction.kernel()
  mp2_energy = mp.MP2(mean_filed_wavefunction).kernel()[0] + hf_energy
  ccsd_wavefunction = cc.RCCSD(mean_filed_wavefunction)
  ccsd_wavefunction.kernel()
  ccsdt_energy = ccsd_wavefunction.ccsd_t() + ccsd_wavefunction.e_tot
  full_ci_wavefunciton = fci.FCI(mean_filed_wavefunction)
  fci_energy, fci_eigenvector = full_ci_wavefunciton.kernel()
  hf_energies.append(hf_energy)
  mp2_energies.append(mp2_energy)
  ccsdt_energies.append(ccsdt_energy)
  fci_energies.append(fci_energy)
  dft_energies.append(dft_energy)
  r_list.append(r)

[15]:

plt.plot(r_list, hf_energies, label="HF")
plt.plot(r_list, mp2_energies, label="MP2")
plt.plot(r_list, ccsdt_energies, label="CCSD(T)")
plt.plot(r_list, fci_energies, label="Full CI")
plt.plot(r_list, dft_energies, label="DFT(B3LYP)")
plt.ylabel("Energy in hartree")
plt.xlabel("H-H distance in angstrom")
plt.legend()
plt.show()
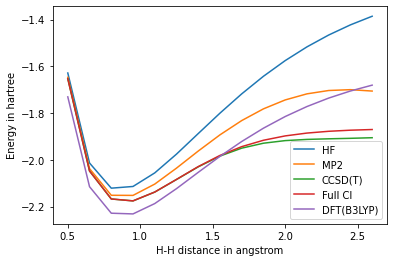
../_images/notebooks_05_01_conventional_quantum_chemical_calculations_15_0.png

DFTは、電子密度に依存する’ad hoc’なポテンシャルをHatree-Fockに導入した理論と捉えることができる。DFT自体は変分法であるが、この追加したポテンシャルのために、DFTのエネルギーの絶対値はFull CIの解よりも低いエネルギーを与えうる。

CCSD(T)は、H-Hの距離が長くなるところ（強相関領域）では、厳密解との乖離が大きくなるが、H-H距離が短いところではFull CIと良好な一致をしめしていることがわかる。

CCSD(T)は優れた理論であり、それ故に’Golden standard’と称されるわけだが、電子相関が強い領域で破綻する（もしくは精度が低下する）ことが知られている。 一般に電子相関が強い領域を定量的に記述することは大変であり、 満足のいく量子化学理論は未だに存在しない。

これが量子コンピュータに期待が集まる背景である。

[ ]:
Contents