[1]:
#!pip install qulacs
#!pip install qulacsvis
#!pip install matplotlib
#!pip install numpy
#!pip install scipy
[2]:
import matplotlib.pyplot as plt
import numpy as np
from qulacs import Observable, QuantumState, QuantumCircuit, ParametricQuantumCircuit, DensityMatrix
from qulacs.gate import X, H, Z, DepolarizingNoise, DephasingNoise, AmplitudeDampingNoise, TwoQubitDepolarizingNoise
リチャードソン外挿法と指数関数外挿法を実装してみる#
以下では、VQEで横磁場イジング模型の基底状態を求め、各ゲートにDepolarizing noiseが作用する状況を考えます。 エラー率を増幅させて、リチャードソン外挿法と指数関数外挿法を実装し、期待値が理想的なものに近づく(=バイアスが減る)ことを確認します。 さらに、サンプリングから期待値を求めた場合には、エラー補償の結果、分散が増大することも確認するのが目的です。
エラーなしの場合#
1次元横磁場イジング模型(\(n=4\)サイト)の基底状態をVQEで求めます。ハミルトニアンは以下のように定義されます。 \begin{align} H=J\sum_{i=1}^nZ_iZ_{i+1}+h\sum_{i=1}^nX_i \end{align} ここでは周期境界条件を仮定し、\(Z_{n+1}=Z_1\)であると約束します。 1次元横磁場イジング模型の基底状態は、パラメータ\(J\)と\(h\)の値によって相転移を示すことが知られています。 このノートブックでは、\(J=h=-1\)のようにパラメータを設定します。
[3]:
#1次元横磁場イジング模型のハミルトニアンを定義
n_qubits = 4
transverse_Ising_hamiltonian = Observable(n_qubits)
J = -1.0
h = -1.0
for i in range(n_qubits):
transverse_Ising_hamiltonian.add_operator(J, f"Z {i} Z {(i+1)%n_qubits}")
transverse_Ising_hamiltonian.add_operator(h, f"X {i}")
次に、VQEのために、パラメータ付きのansatz量子回路\(U(\vec{\theta})\)を定義します。各Y回転ゲートのパラメータ\(\vec{\theta}\)はあとで変化させます。
[4]:
## まずはエラーなしの場合
from qulacsvis import circuit_drawer
from scipy.optimize import minimize
#状態ベクトル、ansatz回路を定義
n_qubits = 4
state = QuantumState(n_qubits)
circuit_depth = 4
circuit = ParametricQuantumCircuit(n_qubits)
#ansatz回路を指定
def Circuit(n_qubits,circuit_depth):
circuit = ParametricQuantumCircuit(n_qubits)
for d in range(circuit_depth):
for i in range(n_qubits):
circuit.add_parametric_RY_gate(i, 0.0)
for i in range(n_qubits):
circuit.add_CZ_gate(i, (i+1)%n_qubits)
return circuit
circuit = Circuit(n_qubits,circuit_depth)
params = np.zeros(circuit.get_parameter_count())
#ansatz回路を表示
circuit_drawer(circuit, "mpl")
[4]:
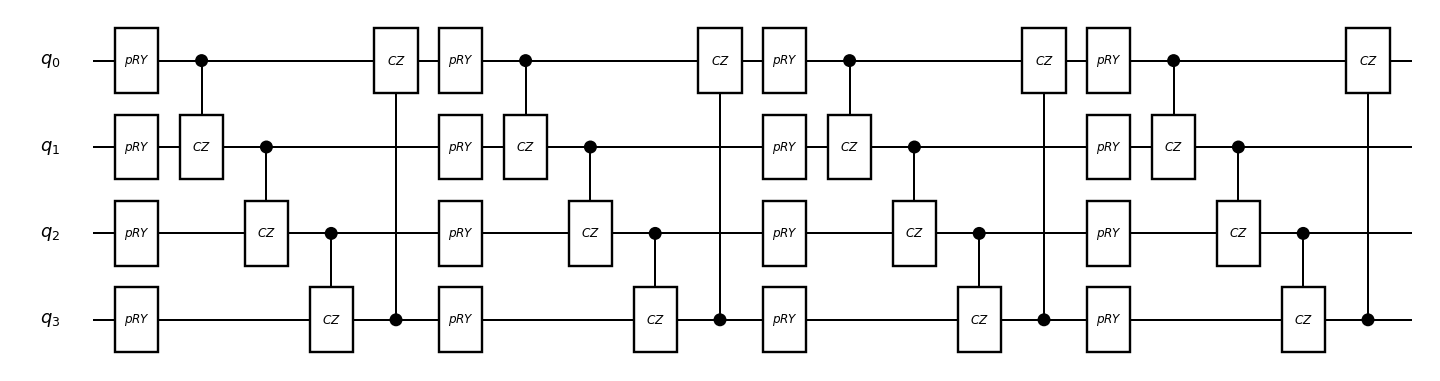
初期状態\(|0^n\rangle\)に、上で定義した量子回路\(U(\vec{\theta})\)を作用させ、ハミルトニアンの期待値を求める関数を定義します。まずはノイズなしの場合を考えているので、状態\(|\psi(\vec{\theta})\rangle= U(\vec{\theta})|0^n\rangle\)を計算し、ハミルトニアンの期待値 \begin{align*} \langle\psi(\vec{\theta})| H |\psi(\vec{\theta})\rangle \end{align*} を求めます。
[5]:
#コスト関数を定義。ここではエネルギー期待値がコスト関数。
def get_cost(params):
state = QuantumState(n_qubits)
for i, p in enumerate(params):
circuit.set_parameter(i,p)
circuit.update_quantum_state(state)
return transverse_Ising_hamiltonian.get_expectation_value(state)
\(\vec{\theta}\)を変化させて、ハミルトニアンの期待値(コスト関数)の最小値 \begin{align*} \min_{\vec{\theta}}\langle\psi(\vec{\theta})| H |\psi(\vec{\theta})\rangle \end{align*} を求めます。
[6]:
#上で定義したansatz回路のもとで、コスト関数を最小化する。
params_initial = np.zeros_like(params)
minimized_costfunction = minimize(get_cost, params_initial, method='BFGS')
exact_energy = transverse_Ising_hamiltonian.solve_ground_state_eigenvalue_by_power_method(state, 50)
#コスト関数の最小値を表示
print("VQEで求めたコスト関数の最小値", minimized_costfunction.fun)
print("基底状態のエネルギー", np.real(exact_energy))
VQEで求めたコスト関数の最小値 -5.072893485692576
基底状態のエネルギー -5.203541892294178
比較のため、べき乗法による計算結果も表示しています。両者は良く一致しており、VQEにより基底状態に近い状態が得られていることが確認できます。
さらに、\(\min_{\vec{\theta}}\langle\psi(\vec{\theta})| H |\psi(\vec{\theta})\rangle\)となるパラメータの値\(\vec{\theta}\)を以下で取得しておきます。
[7]:
#エラーがない場合のansatz回路のパラメータを取得
params_true = minimized_costfunction.x
エラーありの場合#
次にエラーがある場合を考えます。 エラーなしの場合にVQEにより基底状態を計算しましたが、この量子回路にエラーが作用したときに結果がどのように変わるかを調べます。 量子回路はエラーなしの場合と同じにして、CZゲートに以下のエラーを作用させます。
Depolarizing noise: \(\mathcal{E}[\rho]=(1-p)\rho+\frac{p}{3} (X\rho X+Y\rho Y+Z\rho Z)\)
エラーありの場合は、状態ベクトルではなく、密度演算子を使ってシミュレーションをしています。
[8]:
## 次にdepolarizing noiseありの場合(1次元横磁場イジング模型)
#密度演算子、ansatz回路を定義
density_state = DensityMatrix(n_qubits)
noisy_circuit = ParametricQuantumCircuit(n_qubits)
error_rate = 0.01
#ansatz回路を指定
def NoisyCircuit(error_rate):
noisy_circuit = ParametricQuantumCircuit(n_qubits)
for d in range(circuit_depth):
for i in range(n_qubits):
noisy_circuit.add_parametric_RY_gate(i, 0.0)
for i in range(n_qubits):
noisy_circuit.add_CZ_gate(i, (i+1)%n_qubits)
noisy_circuit.add_gate(DepolarizingNoise(i, error_rate))
noisy_circuit.add_gate(DepolarizingNoise((i+1)%n_qubits, error_rate))
return noisy_circuit
noisy_circuit = NoisyCircuit(error_rate)
エラーあり量子回路を密度演算子に作用させて\(\rho(\vec{\theta})\)を計算し、ハミルトニアンの期待値 \begin{align*} {\rm Tr}[\rho(\vec{\theta}) H] \end{align*} を求めます。
[9]:
#コスト関数を定義。ここではエネルギー期待値がコスト関数。
def noisy_get_cost(params):
density_state = DensityMatrix(n_qubits)
for i, p in enumerate(params):
noisy_circuit.set_parameter(i,p)
noisy_circuit.update_quantum_state(density_state)
return transverse_Ising_hamiltonian.get_expectation_value(density_state)
エラーがない場合のansatz回路とパラメータを同じにして、期待値を計算します。
[10]:
#エラーなし、エラーありの場合で期待値を計算
minimized_costfunction_noiseless = get_cost(params_true)
minimized_costfunction_noise = noisy_get_cost(params_true)
#コスト関数の最小値を表示
print("VQEで求めたコスト関数の最小値(エラーなし):", minimized_costfunction_noiseless)
print("VQEで求めたコスト関数の最小値(エラーあり):",minimized_costfunction_noise)
VQEで求めたコスト関数の最小値(エラーなし): -5.072893485692576
VQEで求めたコスト関数の最小値(エラーあり): -4.210928860028173
エラーの影響により、コスト関数の最小値が理想的な場合から遠ざかっていることが確認できます。
エラーを変化させた場合#
コスト関数の期待値のエラー率依存性を求めてみます。
[11]:
data_cost_depolarizingnoise = []
data_noise_strength = []
data_error_rate_per_gate = []
#エラー率を少しずつ変化させて、コスト関数を求める。
for i in range(20):
error_rate=i*0.002
total_error_rate = error_rate * (2.0*n_qubits) * circuit_depth
noisy_circuit = NoisyCircuit(error_rate)
minimized_costfunction_noise = noisy_get_cost(params_true)
data_cost_depolarizingnoise.append(minimized_costfunction_noise)
data_noise_strength.append(total_error_rate)
data_error_rate_per_gate.append(error_rate)
[12]:
#コスト関数 vs (全ゲート数)×(エラー率)のグラフ
plt.plot(data_noise_strength,data_cost_depolarizingnoise, marker="o", linestyle = "--", label=f"expectation value with error")
plt.axhline(minimized_costfunction_noiseless, color="black", linestyle="dashed")
plt.ylabel("energy")
plt.xlabel("total error")
plt.ylim(-5.5,-2.0)
plt.legend()
plt.show()
#(全ゲート数)×(エラー率) vs エラー率のグラフ
plt.plot(data_error_rate_per_gate,data_noise_strength, marker="o", linestyle = "--")
plt.ylabel("total error")
plt.xlabel("error per gate")
plt.show()
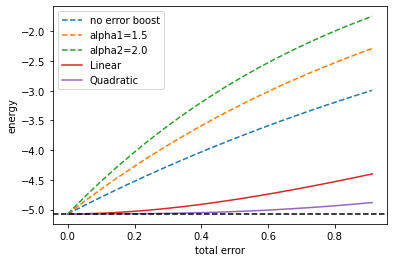
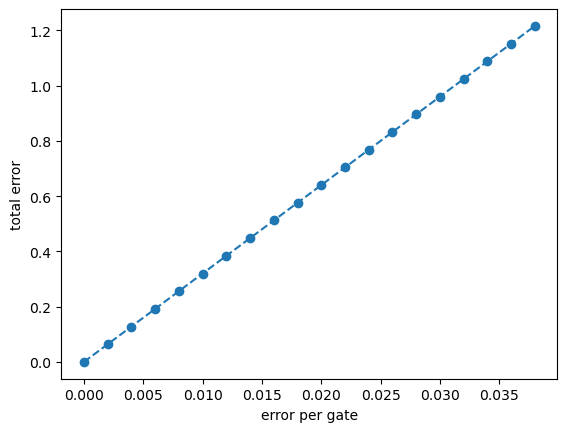
ここで、total error = (全ゲート数)×(エラー率)としました。この値が1程度であれば、測定コストが大きくなりすぎないため、エラー補償は現実的な測定回数で機能します。
外挿法(リチャードソン外挿・指数関数外挿)の実装#
- エラー率を増大させて、外挿法を実装してみます。 まずは線形外挿をやってみます。 エラーの増幅率を\(\alpha(>1)\)、エラー率\(\varepsilon\)のときの期待値を\(\langle H\rangle_\varepsilon\)、エラーを\(\alpha\)倍に増幅したときの期待値を\(\langle H\rangle_{\alpha\varepsilon}\)としたとき、 :nbsphinx-math:`begin{align}
frac{alpha }{alpha -1} langle Hrangle_varepsilon - frac{1 }{alpha -1} langle Hrangle_{alphavarepsilon}
end{align}` を求めます。 計算の手順は以下の通りです。
\(\langle H\rangle_\varepsilon\)を計算(これはすでに実行した)
\(\langle H\rangle_{\alpha\varepsilon}\)を計算
\(\frac{\alpha }{\alpha -1} \langle H\rangle_\varepsilon - \frac{1 }{\alpha -1} \langle H\rangle_{\alpha\varepsilon}\)を計算
[13]:
##error mitigation(外挿法)を実行する。リチャードソン外挿のうち、線形外挿をやってみる。
## ノイズに関するコスト関数のグラフ
data_cost_depolarizingnoise_alpha = []
data_cost_depolarizingnoise_linear_extrapolation = []
alpha = 1.5
for i in range(20):
error_rate=i * 0.002 * alpha
noisy_circuit = NoisyCircuit(error_rate)
minimized_costfunction_noise = noisy_get_cost(params_true)
data_cost_depolarizingnoise_alpha.append(minimized_costfunction_noise)
for i in range(20):
linear_extrapolation = (alpha*data_cost_depolarizingnoise[i]-data_cost_depolarizingnoise_alpha[i])/(alpha - 1.0)
data_cost_depolarizingnoise_linear_extrapolation.append(linear_extrapolation)
[14]:
#線形外挿の結果を表示
plt.plot(data_noise_strength,data_cost_depolarizingnoise, label=f"no error boost",linestyle="dashed")
plt.plot(data_noise_strength,data_cost_depolarizingnoise_alpha, label=f"alpha=1.5",linestyle="dashed")
plt.plot(data_noise_strength,data_cost_depolarizingnoise_linear_extrapolation, label=f"Linear extrapolation")
plt.axhline(minimized_costfunction_noiseless, color="black", linestyle="dashed")
plt.ylabel("energy")
plt.xlabel("total error")
plt.ylim(-5.5,-2.0)
plt.legend()
plt.show()
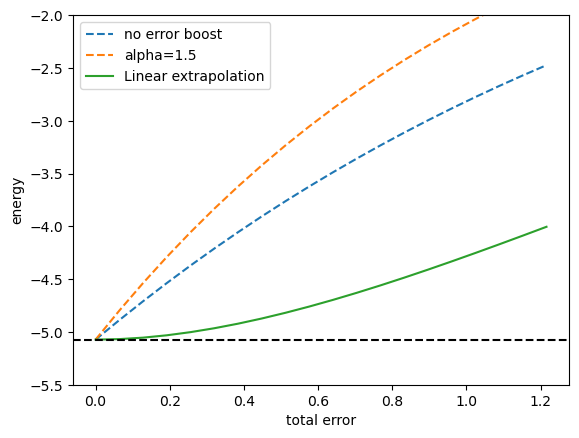
- 次に二次関数で外挿してみます。 エラーの増幅率を\(\alpha_1,\alpha_2(>1)\)としたとき、 :nbsphinx-math:`begin{align}
frac{alpha_1 }{alpha_1 -1}frac{alpha_2 }{alpha_2 -1} langle Hrangle_varepsilon + frac{1 }{1-alpha_1 } frac{alpha_2 }{alpha_2-alpha_1 } langle Hrangle_{alpha_1varepsilon}+ frac{1 }{1-alpha_2 } frac{alpha_1 }{alpha_1-alpha_2 } langle Hrangle_{alpha_2varepsilon}
end{align}` を求めます。
[15]:
##error mitigation(外挿法)を実行する その2(2次多項式で外挿)
## ノイズに関するコスト関数のグラフ
data_cost_depolarizingnoise_alpha2 = []
data_cost_depolarizingnoise_Richardson_extrapolation = []
alpha1 = alpha
alpha2 = 2.0
for i in range(20):
error_rate=i*0.002*alpha2
noisy_circuit = NoisyCircuit(error_rate)
minimized_costfunction_noise = noisy_get_cost(params_true)
data_cost_depolarizingnoise_alpha2.append(minimized_costfunction_noise)
for i in range(20):
beta0 = (alpha1/(alpha1 - 1.0))*(alpha2/(alpha2 - 1.0))
beta1 = ((1.0)/(1.0-alpha1))*(alpha2/(alpha2 - alpha1))
beta2 = ((1.0)/(1.0-alpha2))*(alpha1/(alpha1 - alpha2))
Richardson_extrapolation = beta0*data_cost_depolarizingnoise[i]+beta1*data_cost_depolarizingnoise_alpha[i]+beta2*data_cost_depolarizingnoise_alpha2[i]
data_cost_depolarizingnoise_Richardson_extrapolation.append(Richardson_extrapolation)
[16]:
#実線が外挿した結果、点線はmitigationしていない結果
plt.plot(data_noise_strength,data_cost_depolarizingnoise, label=f"no error boost",linestyle="dashed")
plt.plot(data_noise_strength,data_cost_depolarizingnoise_alpha, label=f"alpha1=1.5",linestyle="dashed")
plt.plot(data_noise_strength,data_cost_depolarizingnoise_alpha2, label=f"alpha2=2.0",linestyle="dashed")
plt.plot(data_noise_strength,data_cost_depolarizingnoise_linear_extrapolation, label=f"Linear")
plt.plot(data_noise_strength,data_cost_depolarizingnoise_Richardson_extrapolation, label=f"Quadratic")
plt.axhline(minimized_costfunction_noiseless, color="black", linestyle="dashed")
plt.ylabel("energy")
plt.xlabel("total error")
plt.ylim(-5.5,-2.0)
plt.legend()
plt.show()
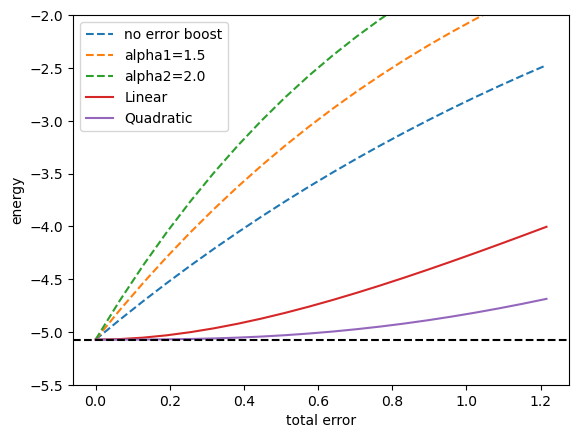
- 1次、2次の多項式で外挿しました。2次で外挿した場合が最もバイアスが小さいことが確認できました。 次に、指数関数外挿も実装します。指数関数外挿とリチャードソン外挿は、測定後のデータ処理の違いのみなので、すでに計算した結果を用います。指数関数外挿の式は以下のようになっています。 :nbsphinx-math:`begin{align}
left[frac{(langle Hrangle_varepsilon)^alpha}{langle Hrangle_{alphavarepsilon}}right]^{frac{1}{alpha-1}}
end{align}`
[17]:
##error mitigation(指数関数外挿法)を実行する その3
## ノイズに関するコスト関数のグラフ
##指数関数外挿とリチャードソン外挿は測定後のデータ処理の違いのみであることに注意
data_cost_depolarizingnoise_Exponential_extrapolation = []
data_cost_depolarizingnoise_Exponential_extrapolation_alpha2 = []
for i in range(20):
Exponential_extrapolation = -np.abs(data_cost_depolarizingnoise[i])**(alpha1/(alpha1 - 1.0)) * np.abs(data_cost_depolarizingnoise_alpha[i])**(1.0/(1.0-alpha1))
data_cost_depolarizingnoise_Exponential_extrapolation.append(Exponential_extrapolation)
for i in range(20):
Exponential_extrapolation = -np.abs(data_cost_depolarizingnoise[i])**(alpha2/(alpha2 - 1.0)) * np.abs(data_cost_depolarizingnoise_alpha2[i])**(1.0/(1.0-alpha2))
data_cost_depolarizingnoise_Exponential_extrapolation_alpha2.append(Exponential_extrapolation)
[18]:
#それぞれ外挿した結果を表示
plt.plot(data_noise_strength,data_cost_depolarizingnoise, label=f"no error boost",linestyle="dashed")
plt.plot(data_noise_strength,data_cost_depolarizingnoise_linear_extrapolation, label=f"Linear")
plt.plot(data_noise_strength,data_cost_depolarizingnoise_Richardson_extrapolation, label=f"Quadratic")
plt.plot(data_noise_strength,data_cost_depolarizingnoise_Exponential_extrapolation, label=f"Exponential")
plt.plot(data_noise_strength,data_cost_depolarizingnoise_Exponential_extrapolation_alpha2, label=f"Exponential alpha2")
plt.axhline(minimized_costfunction_noiseless, color="black", linestyle="dashed")
plt.ylabel("energy")
plt.xlabel("total error")
plt.ylim(-5.5,-2.0)
plt.legend()
plt.show()
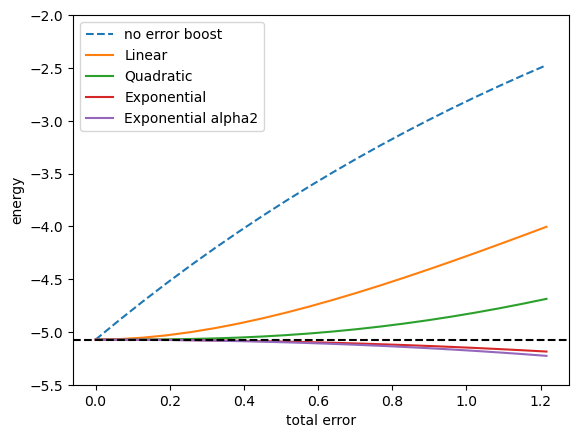
上の例では、指数関数外挿が最も良い結果になっていました。
サンプリングで期待値を求める場合#
get_expectation_valueで期待値を求める代わりに、sampling()を使ってサンプリングから期待値を求めてみます。 その結果を利用して外挿法を実装してみると、エラー補償で分散が增大していることも確認できます。
[19]:
#コスト関数の期待値をサンプリングから求める関数を定義
shots = 3000
def get_cost_sampling(shots,params):
density_state = DensityMatrix(n_qubits)
noisy_circuit = NoisyCircuit(error_rate)
for i, p in enumerate(params):
noisy_circuit.set_parameter(i,p)
noisy_circuit.update_quantum_state(density_state)
density_copy_ZZ = DensityMatrix(n_qubits)
density_copy_X = DensityMatrix(n_qubits)
density_copy_ZZ = density_state.copy()
density_copy_X = density_state.copy()
mask_list_ZZ = [0b1100,0b0110,0b0011,0b1001]
mask_list_X = [0b1000,0b0100,0b0010,0b0001]
for i in range(n_qubits):
gate = H(i)
gate.update_quantum_state(density_copy_X)
noise_sampling_ZZ = density_copy_ZZ.sampling(shots)
noise_sampling_X = density_copy_X.sampling(shots)
estimated_ZZ_average = 0.0
estimated_X_average = 0.0
for s in noise_sampling_ZZ:
for mask in mask_list_ZZ:
bitcount = bin(s & mask).count("1")
estimated_ZZ_average += (-1)**bitcount/shots
for s in noise_sampling_X:
for mask in mask_list_X:
bitcount = bin(s & mask).count("1")
estimated_X_average += (-1)**bitcount/shots
data_sampling_average = h * estimated_X_average + J * estimated_ZZ_average
return data_sampling_average
[20]:
#エラーを変化させて、期待値をサンプリングから求める。
data_cost_depolarizingnoise_sampling1 = []
data_cost_depolarizingnoise_sampling2 = []
data_cost_depolarizingnoise_sampling_linear_extrapolation = []
data_cost_depolarizingnoise_sampling_Exponential_extrapolation = []
alpha = 2.0
#エラーありの期待値(サンプリングで求める)
for i in range(20):
error_rate=i*0.002
density_state = DensityMatrix(n_qubits)
noisy_circuit = NoisyCircuit(error_rate)
minimized_costfunction_noise = get_cost_sampling(shots,params_true)
data_cost_depolarizingnoise_sampling1.append(minimized_costfunction_noise)
#エラーをα倍だけ増幅させたときの期待値(サンプリングで求める)
for i in range(20):
error_rate=i*0.002*alpha
density_state = DensityMatrix(n_qubits)
noisy_circuit = NoisyCircuit(error_rate)
minimized_costfunction_noise = get_cost_sampling(shots,params_true)
data_cost_depolarizingnoise_sampling2.append(minimized_costfunction_noise)
#サンプリングで求めた期待値を使って線形外挿
for i in range(20):
linear_extrapolation = (alpha*data_cost_depolarizingnoise_sampling1[i]-data_cost_depolarizingnoise_sampling2[i])/(alpha - 1.0)
data_cost_depolarizingnoise_sampling_linear_extrapolation.append(linear_extrapolation)
#サンプリングで求めた期待値を使って指数関数外挿
for i in range(20):
Exponential_extrapolation_sampling = -np.abs(data_cost_depolarizingnoise_sampling1[i])**(alpha/(alpha - 1.0)) * np.abs(data_cost_depolarizingnoise_sampling2[i])**(1.0/(1.0-alpha))
data_cost_depolarizingnoise_sampling_Exponential_extrapolation.append(Exponential_extrapolation_sampling)
[21]:
#厳密な期待値を使った結果と、サンプリングを使った結果をそれぞれグラフに表示させる
plt.plot(data_noise_strength,data_cost_depolarizingnoise, label=f"no error boost",linestyle="dashed")
#plt.plot(data_noise_strength,data_cost_depolarizingnoise_alpha2, label=f"alpha2=2.0",linestyle="dashed")
plt.plot(data_noise_strength,data_cost_depolarizingnoise_linear_extrapolation, label=f"Linear",linestyle="dashed")
#plt.plot(data_noise_strength,data_cost_depolarizingnoise_Richardson_extrapolation, label=f"Quadratic")
plt.plot(data_noise_strength,data_cost_depolarizingnoise_Exponential_extrapolation_alpha2, label=f"Exponential alpha2",linestyle="dashed")
plt.plot(data_noise_strength,data_cost_depolarizingnoise_sampling1, label=f"no error boost sampling")
#plt.plot(data_noise_strength,data_cost_depolarizingnoise_sampling2, label=f"alpha=2.0, sampling")
plt.plot(data_noise_strength,data_cost_depolarizingnoise_sampling_linear_extrapolation, label=f"Linear extrapolation sampling")
plt.plot(data_noise_strength,data_cost_depolarizingnoise_sampling_Exponential_extrapolation, label=f"Exponential extrapolation sampling")
plt.axhline(minimized_costfunction_noiseless, color="black", linestyle="dashed")
plt.ylabel("energy")
plt.xlabel("total error")
plt.ylim(-5.5,-2.0)
plt.legend()
plt.show()
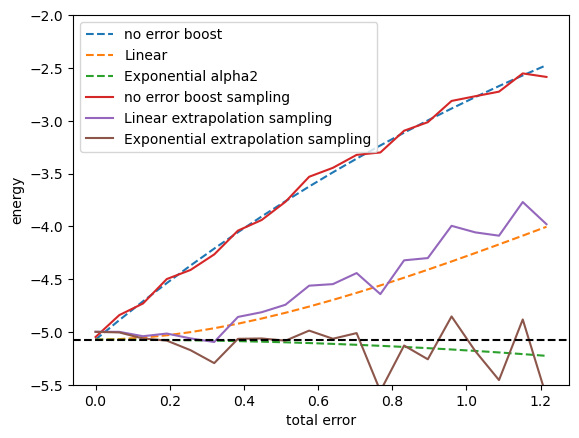
測定回数\(3000\times 2\)の場合について計算してみました。点線が期待値そのもの、実線がサンプリングした場合を表しています。error mitigationした結果はエラー率が増大するにつれ、分散が増大していることが確認できます。この分散を抑えるためには、測定回数を増やす必要があります。
[22]:
#エラー率を固定して、ヒストグラムを作成
error_rate = 0.04
n_test = 1000
shots = 1000
alpha1 = 1.3
total_error_rate = error_rate * (3.0*n_qubits) * circuit_depth
no_mitigation_list = np.zeros(n_test)
error_boost_list = np.zeros(n_test)
linear_mitigated_list = np.zeros(n_test)
exponential_mitigated_list = np.zeros(n_test)
for i in range(n_test):
density_state = DensityMatrix(n_qubits)
noisy_circuit = NoisyCircuit(error_rate)
no_mitigation_list[i] = get_cost_sampling(shots,params_true)
expec_value = noisy_get_cost(params_true)
error_rate = error_rate *alpha1
for i in range(n_test):
density_state = DensityMatrix(n_qubits)
noisy_circuit = NoisyCircuit(error_rate*alpha1)
error_boost_list[i] = get_cost_sampling(shots,params_true)
for i in range(n_test):
linear_mitigated_list[i] = (alpha1*no_mitigation_list[i]-error_boost_list[i])/(alpha1 - 1.0)
exponential_mitigated_list[i] = - np.abs(no_mitigation_list[i])**(alpha1/(alpha1 - 1.0)) * np.abs(error_boost_list[i])**(1.0/(1.0-alpha1))
[23]:
plt.hist(no_mitigation_list, alpha=0.2, bins=20, label=f"no error boost")
plt.hist(linear_mitigated_list, alpha=0.2, bins=20, label=f"Linear")
plt.hist(exponential_mitigated_list, alpha=0.2, bins=20, label=f"Exponential")
plt.axvline(expec_value, color="black")
plt.axvline(get_cost(params_true), color="red")
plt.legend(loc="upper left", fontsize=13)
plt.show()
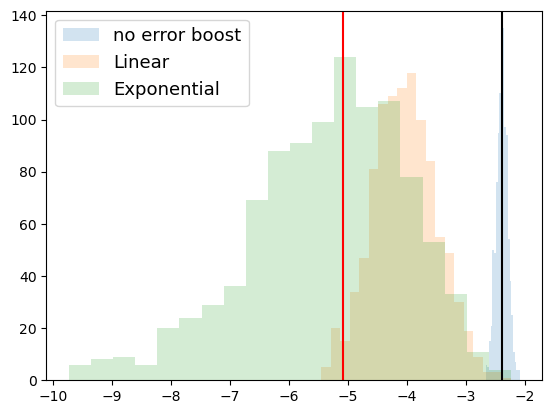
エラー率を固定して、ヒストグラムを作成した結果です。 指数関数外挿が最もエラーを抑制できていることが分かります。 一方で、分散もそのぶん増大していることも分かります。
[24]:
#得られたヒストグラムから、それぞれの標準偏差を求めてみる。標準偏差の比から測定コストが求まる。
std_no_mitigation = np.std(no_mitigation_list)
std_linear_extrapolation = np.std(linear_mitigated_list)
std_exponential_extrapolation = np.std(exponential_mitigated_list)
[25]:
#理論的に見積もられる測定コスト
cost_linear_extrapolation = np.sqrt((alpha1/(alpha1 - 1.0))**2 + (1.0/(alpha1 - 1.0))**2)
cost_exponential_extrapolation = np.sqrt((alpha1/(alpha1 - 1.0)*np.exp(total_error_rate))**2 + (1.0/(alpha1 - 1.0)*np.exp(alpha1*total_error_rate))**2)
[26]:
#計算して得られた標準偏差の増加分と、コストの見積もりの比較・線形外挿
print("計算して得られた標準偏差の増加分:", std_linear_extrapolation/std_no_mitigation)
print("理論式から求めた測定コスト:",cost_linear_extrapolation)
計算して得られた標準偏差の増加分: 5.537282728428462
理論式から求めた測定コスト: 5.467073155618908
[27]:
#計算して得られた標準偏差の増加分と、コストの見積もりの比較・指数関数外挿
print("計算して得られた標準偏差の増加分:",std_exponential_extrapolation/std_no_mitigation)
print("理論式から求めた測定コスト:",cost_exponential_extrapolation)
計算して得られた標準偏差の増加分: 13.729151856744801
理論式から求めた測定コスト: 50.09531384324509
測定コストの理論式は、リチャードソン外挿だとほぼ同じ値になるのに対し、指数関数外挿は少し大きめの値になっていることが分かりました。
[ ]:
