[1]:

#!pip install qulacs
#!pip install qulacsvis
#!pip install matplotlib
#!pip install numpy
#!pip install scipy

[2]:

import matplotlib.pyplot as plt
import numpy as np
from qulacs import Observable, QuantumState, DensityMatrix, GeneralQuantumOperator
from qulacs.gate import  X, H, Z, DepolarizingNoise, DephasingNoise, AmplitudeDampingNoise, TwoQubitDepolarizingNoise, NoisyEvolution_fast

Qulacsでの混合状態#

DensityMatrixクラス：qulacsでの密度演算子（混合状態）の取り扱い#

量子状態（密度演算子）の準備
密度演算子をnumpyのarrayに変換、あるいはその逆：get_matrix(), load()
いくつかのエラー：DepolarizingNoiseなど
計算基底でのサンプリング：sampling()
Lindblad方程式のシミュレーション：NoisyEvolution_fast()

量子状態（密度演算子）の準備#

Qulacs上で密度演算子を準備するには、DensityMatrixを使います。引数は量子ビット数になっていて、量子ビット数\(n\)に対して、\(2^n\times 2^n(=2^{2n})\)の行列が定義されます。同じ量子ビット数でも、状態ベクトルを使ったシミュレーションに比べて要素数が多いので、量子ビット数が多いときには扱いづらいことに注意。

[3]:

#密度演算子を準備
n_qubits = 1
density_matrix = DensityMatrix(n_qubits)
print("Qulacsで密度演算子を定義","\n",density_matrix)

Qulacsで密度演算子を定義
  *** Density Matrix ***
 * Qubit Count : 1
 * Dimension   : 2
 * Density matrix :
(1,0) (0,0)
(0,0) (0,0)

初期状態は\(|0\rangle\langle 0|\)になっている。行列成分の\((0,0)\)成分が1で残りの成分がすべて0になっていることからも分かる。

密度演算子をnumpyのarrayに変換、あるいはその逆：#

それぞれget_matrix(), load()を使って変換することが可能。

[4]:

#numpy arrayからqulacsのDensityMatrixへ変換
mat = np.array([[0.5, 0.5], [0.5, 0.5]])
density_matrix.load(mat)
print(density_matrix)

dm = density_matrix.get_matrix()
print(dm)

 *** Density Matrix ***
 * Qubit Count : 1
 * Dimension   : 2
 * Density matrix :
(0.5,0) (0.5,0)
(0.5,0) (0.5,0)

[[0.5+0.j 0.5+0.j]
 [0.5+0.j 0.5+0.j]]

※上の量子状態は、実は純粋状態\(|+\rangle=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\)になっています。\(|+\rangle\langle+|\)を表示してみれば一致することが確認できます。

すべて0状態へ初期化するには、状態ベクトルの場合と同じくset_zero_state()で行います。

[5]:

density_matrix.set_zero_state()
print(density_matrix)

 *** Density Matrix ***
 * Qubit Count : 1
 * Dimension   : 2
 * Density matrix :
(1,0) (0,0)
(0,0) (0,0)

いくつかのエラー：`DepolarizingNoise`など#

Qulacsで代表的なノイズを作用させてみます。まずは、Depolarizing noise: \(\mathcal{E}[\rho]=(1-p)\rho+\frac{p}{3} (X\rho X+Y\rho Y+Z\rho Z)\) (\(0\le p \le 0.75\))。入力を \begin{equation*} \rho=|+\rangle\langle+|= \begin{pmatrix} 0.5 & 0.5\\ 0.5 & 0.5 \end{pmatrix} \end{equation*} のようにして、\(p = 0.15\)で \begin{equation*} \mathcal{E}[\rho]= \begin{pmatrix} 0.5 & 0.4\\ 0.4 & 0.5 \end{pmatrix} \end{equation*} となることを確認してみます。

[6]:

#depolarizing noiseを作用
density_matrix.load(mat)
p = 0.15
gate = DepolarizingNoise(0, p)
gate.update_quantum_state(density_matrix)
print(density_matrix)

 *** Density Matrix ***
 * Qubit Count : 1
 * Dimension   : 2
 * Density matrix :
(0.5,0) (0.4,0)
(0.4,0) (0.5,0)

Dephasing noise: \(\mathcal{E}[\rho]=(1-p)\rho +p Z\rho Z\) (\(0\le p \le 0.5\))

[7]:

#dephasing noiseを作用
density_matrix.load(mat)

p=0.3
gate = DephasingNoise(0, p)
gate.update_quantum_state(density_matrix)
print(density_matrix)

 *** Density Matrix ***
 * Qubit Count : 1
 * Dimension   : 2
 * Density matrix :
(0.5,0) (0.2,0)
(0.2,0) (0.5,0)

２量子ビットの場合で、各量子ビットにdepolarizing noiseを作用させます。

[8]:

#２量子ビットの場合：depolarizing noiseを作用
density_matrix_2 = DensityMatrix(2)
p = 0.15
gate = DepolarizingNoise(0, p)
gate.update_quantum_state(density_matrix_2)
gate = DepolarizingNoise(1, p)
gate.update_quantum_state(density_matrix_2)
print(density_matrix_2)

 *** Density Matrix ***
 * Qubit Count : 2
 * Dimension   : 4
 * Density matrix :
(0.81,0)    (0,0)    (0,0)    (0,0)
   (0,0) (0.09,0)    (0,0)    (0,0)
   (0,0)    (0,0) (0.09,0)    (0,0)
   (0,0)    (0,0)    (0,0) (0.01,0)

密度演算子で期待値を求めたい場合は、状態ベクトルの場合と同じくget_expectation_value(state)を使えばOK。以下の例では、amplitude damping noiseを作用させた後の密度演算子\(\rho\)に対し、パウリ\(Z\)の期待値\({\rm Tr}[\rho Z]\)を求めています。

[9]:

#Amplitude damping noiseを作用させた後、Zの期待値を計算
density_matrix.load(mat)

#Amplitude damping noiseを作用
p=0.15
gate = AmplitudeDampingNoise(0, p)
gate.update_quantum_state(density_matrix)

#Zの期待値を計算
Z0 = Observable(n_qubits)
Z0.add_operator(1.0, "Z 0")
expec = Z0.get_expectation_value(density_matrix)
print(density_matrix)
print("Zの期待値", expec)

 *** Density Matrix ***
 * Qubit Count : 1
 * Dimension   : 2
 * Density matrix :
   (0.575,0) (0.460977,0)
(0.460977,0)    (0.425,0)

Zの期待値 0.1499999999999999

ここまでは、qulacs上で密度演算子にエラーを作用させることを考えました。一方で、qulacs上で状態ベクトル（純粋状態）に作用させると、確率的にエラーが作用した状態ベクトルを返します。例えば、Depolarizing noiseだと、確率\((1-p)\)で入力した状態をそのまま返し、確率\(p/3\)でそれぞれX、Y、Zゲートが作用した状態が確率的に得られます。実行するたびにランダムに状態ベクトルが選ばれることに注意。

[10]:

#状態ベクトルにDepolarizingNoiseなどを作用させると、確率的に状態ベクトルが得られる
state = QuantumState(n_qubits)
vec = np.array([0.0,1.0])
print("初期状態",state.get_vector())

p=0.5
gate = DepolarizingNoise(0, p)

#状態ベクトルvecを用意→DepolarizingNoiseを複数回作用させてみる
for i in range(5):
    state.load(vec)
    gate.update_quantum_state(state)
    print("{}回目".format(i+1),state.get_vector())

初期状態 [1.+0.j 0.+0.j]
1回目 [ 0.+0.j -1.-0.j]
2回目 [ 0.-1.j -0.+0.j]
3回目 [ 0.-1.j -0.+0.j]
4回目 [0.+0.j 1.+0.j]
5回目 [0.+0.j 1.+0.j]

確率的に選ばれるため、ノイズが作用した状況のもとで所望の量（期待値など）を求めるためには、同じ計算を何度も実行して平均する必要があります（密度演算子から期待値を計算する場合は、平均操作は不要）。ノイズあり期待値を状態ベクトルで計算する場合は、量子ビット数が大きく取った大規模なシミュレーションを行なう際に用います。

計算基底でのサンプリング：#

sampling()を用いる。qulacs上で定義した密度演算子に使うことで、測定結果に相当するビット列が得られます。統計誤差を含むシミュレーションをする場合に用います。

[11]:

#密度演算子からサンプリング
shots = 20
mat2 = np.array([[0.9, 0.0], [0.0, 0.1]])
density_matrix.load(mat2)
noiseless_sampling = density_matrix.sampling(shots)

print("サンプリングで得られたビット列",noiseless_sampling)
print(density_matrix)

サンプリングで得られたビット列 [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0]
 *** Density Matrix ***
 * Qubit Count : 1
 * Dimension   : 2
 * Density matrix :
(0.9,0)   (0,0)
  (0,0) (0.1,0)

0が出る確率が\(\langle 0 |\rho |0\rangle\)で、1が出る確率が\(\langle 1 |\rho |1\rangle\)になります（ボルンの確率規則）。これらは、密度演算子の対角項の値そのものです。上の例では、0が出る確率が0.9、1が出る確率が0.1であることを意味します。以下では、測定結果から期待値を推定することを考えます。

[12]:

#サンプリングにより物理量Zの平均値を求める
shots = 100

#エラーなしの場合
noiseless_sampling = density_matrix.sampling(shots)

estimated_Z_average = 0.0
#物理量Zのサンプリングからの平均値は、測定結果がゼロのときは＋１、測定結果が１のときは－１を加える→サンプリング回数で割る、のようにして求める
for i in range(shots):
    estimated_Z_average += (-2*noiseless_sampling[i]+1)/shots

#物理量Zの期待値とサンプリングからの平均値を比較してみる
print("エラーなしの場合")
print("サンプリングから推定したZの平均値",estimated_Z_average)
print("Zの期待値",Z0.get_expectation_value(density_matrix))

エラーなしの場合
サンプリングから推定したZの平均値 0.8600000000000005
Zの期待値 0.8

上の例では、パウリ\(Z\)の期待値を計算しています。\(Z=|0\rangle\langle 0|- |1\rangle\langle 1|\)であることを使って :nbsphinx-math:`begin{equation*}: {rm Tr}[rho Z]= langle 0 |rho |0rangle- langle 1 |rho |1rangle

end{equation*}` という関係が導けます。 0が出る確率が\(\langle 0 |\rho |0\rangle\)で、1が出る確率が\(\langle 1 |\rho |1\rangle\)であったことを思い出すと、サンプリング結果から平均値は \begin{equation*} {\rm (平均値)}= \frac{({\rm 0が出た回数})}{({\rm 測定回数})}-\frac{({\rm 1が出た回数})}{({\rm 測定回数})} \end{equation*} のようにすれば推定可能です。あるいは、測定結果がゼロのときは＋１、測定結果が１のときは－１となることから \begin{equation*} {\rm (平均値)}= \frac{({\rm すべての測定結果の総和})}{({\rm 測定回数})} \end{equation*} のように計算してもOKです。

[13]:

#binを使って平均値を計算
estimated_Z_average = 0.0
for s in noiseless_sampling:
    bitcount = bin(s & 0b1).count("1")
    estimated_Z_average += (-1)**bitcount/shots
print(estimated_Z_average)

0.8600000000000005

このように推定して得られた結果は、統計誤差を含むため、厳密な期待値とは一致しません。このことを確認するために、何度も平均値を求めてヒストグラムを作成してみます。

[14]:

#ヒストグラムを作成
n_test = 1000
shots = 1000
noiseless_list = np.zeros(n_test)

for i in range(n_test):
    noiseless_sampling = density_matrix.sampling(shots)
    estimated_Z_average = 0.0
    for j in range(shots):
        estimated_Z_average += (-2*noiseless_sampling[j]+1)/shots
    noiseless_list[i] = estimated_Z_average
noiseless_expec_value = Z0.get_expectation_value(density_matrix)

[15]:

plt.hist(noiseless_list, alpha=0.2, bins=20, label=f"Noiseless")
plt.axvline(noiseless_expec_value, color="black")
plt.legend(loc="upper left", fontsize=13)
plt.show()

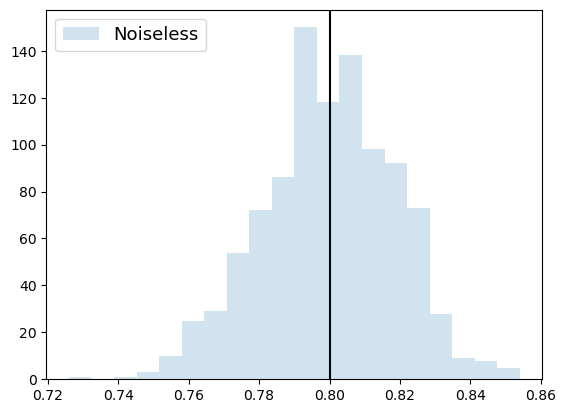
../_images/notebooks_04_01_Density_Matrix_and_Error_32_0.png

エラーがある場合についてもヒストグラムを求めてみます。

[16]:

#サンプリングにより物理量の平均値を求める
shots = 100

#エラーありの場合
p = 0.3
gate = DepolarizingNoise(0, p)
gate.update_quantum_state(density_matrix)
noise_sampling = density_matrix.sampling(shots)

estimated_Z_average = 0.0
#物理量Zのサンプリングからの平均値は、測定結果がゼロのときは＋１、測定結果が１のときは－１を加える→サンプリング回数で割る、のようにして求める
for i in range(shots):
    estimated_Z_average += (-2*noise_sampling[i]+1)/shots

#物理量Zの期待値とサンプリングからの平均値を比較してみる
print("エラーがある場合")
print("サンプリングから推定したZの平均値",estimated_Z_average)
print("Zの期待値",Z0.get_expectation_value(density_matrix))

エラーがある場合
サンプリングから推定したZの平均値 0.46000000000000024
Zの期待値 0.48

[17]:

#ヒストグラムを作成
n_test = 1000
shots = 1000
noisy_list = np.zeros(n_test)

for i in range(n_test):
    noisy_sampling = density_matrix.sampling(shots)
    estimated_Z_average = 0.0
    for j in range(shots):
        estimated_Z_average += (-2*noisy_sampling[j]+1)/shots
    noisy_list[i] = estimated_Z_average
noisy_expec_value = Z0.get_expectation_value(density_matrix)

[18]:

plt.hist(noiseless_list, alpha=0.2, bins=20, label=f"Noiseless")
plt.hist(noisy_list, alpha=0.2, bins=20, label=f"Noisy")
plt.axvline(noiseless_expec_value, color="black")
plt.axvline(noisy_expec_value, color="red")
plt.legend(loc="upper left", fontsize=13)
plt.show()

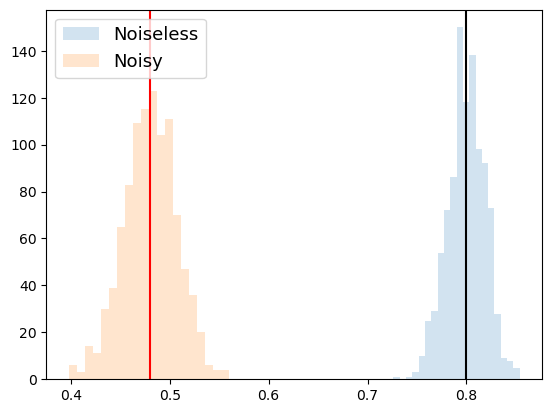
../_images/notebooks_04_01_Density_Matrix_and_Error_36_0.png

講義で説明したような図が得られました。期待値の推定は統計誤差を含むこと、ノイズの影響で期待値が変化する（＝バイアスが生じる）ことが確認できます。

２量子ビットの場合でも、サンプリングから期待値を推定してみます。

[19]:

#２量子ビットの場合の密度演算子からサンプリング
shots = 300
mat3 = np.array([[0.5, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.3, 0.0], [0.0, 0.0, 0.0, 0.2]])
density_matrix_2.load(mat3)
noiseless_sampling_2 = density_matrix_2.sampling(shots)

print("サンプリングで得られたビット列",noiseless_sampling_2)
print(density_matrix_2)

サンプリングで得られたビット列 [3, 0, 3, 0, 0, 2, 3, 3, 0, 3, 3, 0, 0, 0, 0, 0, 2, 3, 3, 3, 0, 0, 2, 0, 0, 0, 0, 0, 0, 2, 2, 3, 3, 0, 0, 0, 0, 0, 2, 0, 2, 3, 0, 2, 0, 3, 2, 3, 0, 0, 3, 0, 0, 2, 3, 0, 0, 0, 2, 3, 0, 2, 3, 0, 3, 3, 0, 0, 0, 3, 0, 0, 0, 2, 0, 3, 0, 0, 2, 2, 0, 0, 2, 0, 0, 2, 0, 0, 2, 0, 0, 0, 2, 3, 2, 0, 3, 0, 2, 3, 3, 0, 2, 3, 2, 3, 0, 3, 0, 0, 0, 0, 2, 2, 0, 0, 0, 0, 2, 2, 0, 0, 0, 0, 3, 2, 0, 3, 2, 2, 0, 3, 2, 0, 2, 0, 3, 0, 3, 0, 3, 3, 2, 2, 2, 2, 0, 0, 3, 0, 3, 2, 2, 0, 3, 0, 0, 0, 2, 0, 0, 2, 3, 0, 3, 3, 2, 0, 0, 2, 2, 2, 0, 0, 0, 0, 2, 2, 3, 2, 0, 0, 3, 0, 3, 2, 2, 3, 2, 2, 2, 0, 0, 2, 0, 3, 0, 3, 0, 0, 3, 0, 0, 3, 3, 2, 3, 0, 0, 2, 3, 0, 0, 0, 2, 0, 3, 0, 2, 2, 2, 3, 0, 2, 2, 0, 0, 3, 3, 3, 2, 0, 0, 2, 3, 2, 0, 0, 0, 0, 2, 2, 0, 0, 0, 3, 2, 2, 0, 0, 2, 0, 0, 3, 3, 2, 0, 2, 0, 0, 0, 0, 0, 2, 0, 0, 2, 3, 2, 0, 0, 0, 0, 0, 2, 0, 0, 0, 2, 2, 3, 2, 2, 0, 2, 2, 3, 2, 3, 0, 0, 2, 0, 3, 2, 0, 0, 0, 0, 0]
 *** Density Matrix ***
 * Qubit Count : 2
 * Dimension   : 4
 * Density matrix :
(0.5,0)   (0,0)   (0,0)   (0,0)
  (0,0)   (0,0)   (0,0)   (0,0)
  (0,0)   (0,0) (0.3,0)   (0,0)
  (0,0)   (0,0)   (0,0) (0.2,0)

測定結果はゼロ以上の整数（上の例なら、0, 2, 3のどれか）が得られます。２進数表示したときのビット列が、各量子ビットの測定結果に対応しています。２量子ビットの場合は以下の通り。 \begin{align*} 0 &\rightarrow 00\\ 1 &\rightarrow 01\\ 2 &\rightarrow 10\\ 3 &\rightarrow 11\\ \end{align*} pythonで１０進数を２進数に変換するには、bin()を使えばOK。

[21]:

#bin()を使ってサンプリング結果を２進数に変換。0bは２進数を意味します。
print([bin(n) for n in noiseless_sampling_2])

['0b11', '0b0', '0b11', '0b0', '0b0', '0b10', '0b11', '0b11', '0b0', '0b11', '0b11', '0b0', '0b0', '0b0', '0b0', '0b0', '0b10', '0b11', '0b11', '0b11', '0b0', '0b0', '0b10', '0b0', '0b0', '0b0', '0b0', '0b0', '0b0', '0b10', '0b10', '0b11', '0b11', '0b0', '0b0', '0b0', '0b0', '0b0', '0b10', '0b0', '0b10', '0b11', '0b0', '0b10', '0b0', '0b11', '0b10', '0b11', '0b0', '0b0', '0b11', '0b0', '0b0', '0b10', '0b11', '0b0', '0b0', '0b0', '0b10', '0b11', '0b0', '0b10', '0b11', '0b0', '0b11', '0b11', '0b0', '0b0', '0b0', '0b11', '0b0', '0b0', '0b0', '0b10', '0b0', '0b11', '0b0', '0b0', '0b10', '0b10', '0b0', '0b0', '0b10', '0b0', '0b0', '0b10', '0b0', '0b0', '0b10', '0b0', '0b0', '0b0', '0b10', '0b11', '0b10', '0b0', '0b11', '0b0', '0b10', '0b11', '0b11', '0b0', '0b10', '0b11', '0b10', '0b11', '0b0', '0b11', '0b0', '0b0', '0b0', '0b0', '0b10', '0b10', '0b0', '0b0', '0b0', '0b0', '0b10', '0b10', '0b0', '0b0', '0b0', '0b0', '0b11', '0b10', '0b0', '0b11', '0b10', '0b10', '0b0', '0b11', '0b10', '0b0', '0b10', '0b0', '0b11', '0b0', '0b11', '0b0', '0b11', '0b11', '0b10', '0b10', '0b10', '0b10', '0b0', '0b0', '0b11', '0b0', '0b11', '0b10', '0b10', '0b0', '0b11', '0b0', '0b0', '0b0', '0b10', '0b0', '0b0', '0b10', '0b11', '0b0', '0b11', '0b11', '0b10', '0b0', '0b0', '0b10', '0b10', '0b10', '0b0', '0b0', '0b0', '0b0', '0b10', '0b10', '0b11', '0b10', '0b0', '0b0', '0b11', '0b0', '0b11', '0b10', '0b10', '0b11', '0b10', '0b10', '0b10', '0b0', '0b0', '0b10', '0b0', '0b11', '0b0', '0b11', '0b0', '0b0', '0b11', '0b0', '0b0', '0b11', '0b11', '0b10', '0b11', '0b0', '0b0', '0b10', '0b11', '0b0', '0b0', '0b0', '0b10', '0b0', '0b11', '0b0', '0b10', '0b10', '0b10', '0b11', '0b0', '0b10', '0b10', '0b0', '0b0', '0b11', '0b11', '0b11', '0b10', '0b0', '0b0', '0b10', '0b11', '0b10', '0b0', '0b0', '0b0', '0b0', '0b10', '0b10', '0b0', '0b0', '0b0', '0b11', '0b10', '0b10', '0b0', '0b0', '0b10', '0b0', '0b0', '0b11', '0b11', '0b10', '0b0', '0b10', '0b0', '0b0', '0b0', '0b0', '0b0', '0b10', '0b0', '0b0', '0b10', '0b11', '0b10', '0b0', '0b0', '0b0', '0b0', '0b0', '0b10', '0b0', '0b0', '0b0', '0b10', '0b10', '0b11', '0b10', '0b10', '0b0', '0b10', '0b10', '0b11', '0b10', '0b11', '0b0', '0b0', '0b10', '0b0', '0b11', '0b10', '0b0', '0b0', '0b0', '0b0', '0b0']

bin()を使って、\(Z_0Z_1\)の期待値を計算してみます。

[22]:

estimated_ZZ_average = 0.0
for s in noiseless_sampling_2:
    bitcount = bin(s & 0b11).count("1")
    estimated_ZZ_average += (-1)**bitcount/shots
Z0Z1 = Observable(2)
Z0Z1.add_operator(1.0, "Z 0 Z 1")
print("サンプリングから推定した平均値",estimated_ZZ_average)
print("ZZの期待値",Z0Z1.get_expectation_value(density_matrix_2))

サンプリングから推定した平均値 0.4400000000000009
ZZの期待値 0.4

\(Z_0Z_1\)は、測定結果に対して値を \begin{align*} 00 &\rightarrow (+1)\\ 01 &\rightarrow (-1)\\ 10 &\rightarrow (-1)\\ 11 &\rightarrow (+1)\\ \end{align*} のように割り当てて平均値を計算しています。 \(1\)が偶数個だと(+1)、奇数個だと(-1)となっていますが、この値は、\(Z_0Z_1\)の固有値を意味しています。この割り当ては、上のセルのbin(s & 0b11).count("1")および(-1)**bitcountの部分に対応しています。

Lindblad方程式のシミュレーション：`NoisyEvolution_fast()`#

環境からの影響を取り入れた量子開放系のダイナミクスのシミュレーションを行ないます。方程式は以下の通りです。 \begin{align} \frac{d}{dt} \rho(t) = -i[H,\rho(t)] +\sum_k \left(L_k \rho(t) L_k^\dagger -\frac{1}{2}L_k^\dagger L_k \rho(t)-\frac{1}{2} \rho(t)L_k^\dagger L_k\right). \end{align} ここで、\(\rho(t)\)は時刻\(t\)における系の密度演算子、\(H\)はハミルトニアン、\(L_k\)はリンドブラッド演算子です。簡単な例として、以下の１量子ビット系の場合を考えます。 \begin{align} \frac{d}{dt} \rho(t) = -iJ[Z,\rho(t)] +\gamma \left(Z \rho(t) Z -\rho(t)\right). \end{align} \(H=JZ\), \(L_k = \sqrt{\gamma}Z\)として、\(k\)は一つだけの場合をシミュレーションします。初期状態は\(|+\rangle\)として時間発展した場合、時刻\(t\)における物理量\(X\)の期待値は以下のようになります。 \begin{align} \langle X\rangle_t = e^{-2\gamma t} \cos{2Jt} \end{align} このことを以下のシミュレーションで実行して、確認してみます。

[23]:

#qulacsを使ったLindblad方程式のシミュレーション
n = 1
T = 1.5
element = 40
tlist = np.linspace(0, T, element)

#物理量はXにする
observable = Observable(n)
observable.add_operator(1., "X 0")

#HamiltonianはZとする
hamiltonian = Observable(n)
J = 5.0
hamiltonian.add_operator(J, "Z 0 ")

#Lindblad演算子を指定
decay_rate_z = 0.3
c_ops = [GeneralQuantumOperator(n) for _ in range(n)]
c_ops[0].add_operator(np.sqrt(decay_rate_z), "Z 0")

#期待値をサンプリングにより求める
n_samples = 100
state = QuantumState(n)
exp_list = []
exp2_list = []
for t in tlist:
    exp = np.zeros(n_samples)
    for i in range(n_samples):
        state.set_zero_state()
        H(0).update_quantum_state(state)
        gate = NoisyEvolution_fast(hamiltonian, c_ops, t)
        gate.update_quantum_state(state)
        exp[i] = observable.get_expectation_value(state)
    exp_list.append(np.average(exp))
    exp2_list.append(np.std(exp)/np.sqrt(n_samples))

[24]:

plt.figure()
plt.errorbar(tlist, exp_list, exp2_list, capsize=5, fmt='o',label=f"sampling")
plt.plot(tlist,np.exp(-2.0*decay_rate_z*tlist)*np.cos(2.0*J*tlist),label=f"exact")
plt.ylabel("Expectation values")
plt.xlabel("Time")
plt.legend()
plt.show()

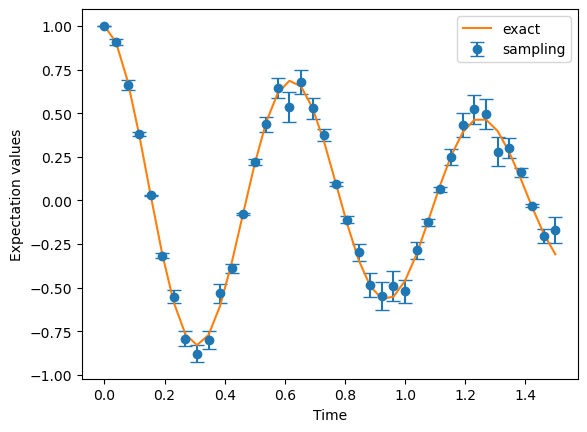
../_images/notebooks_04_01_Density_Matrix_and_Error_48_0.png

QulacsではLindbladによる時間発展をモンテカルロ的に実行しているので、何度も実行して平均を取る必要があります。

練習#

２つの量子状態（純粋状態\(|\psi\rangle=\sqrt{\frac{3}{4}}|0\rangle+\sqrt{\frac{1}{4}}|1\rangle\)、混合状態\(\rho=\frac{3}{4}|0\rangle\langle0|+\frac{1}{4}|1\rangle\langle1|\)）に対して、物理量の期待値XとZを求めてみましょう。
２量子ビットの場合で、ノイズが作用した状態（密度演算子）を作成してみましょう。DepolarizingNoiseが１量子ビット目と２量子ビット目に作用した状態と、TwoQubitDepolarizingNoiseが作用した状態が一般に異なることを確認してください。

補足：#

変分量子アルゴリズムなどでは、QuantumCircuit, ParametricQuantumCircuitを使いますが、このときcircuit.add_gate(DepolarizingNoise(0, 0.15))のように使えばOK。

[25]:

from qulacs import QuantumCircuit,  ParametricQuantumCircuit

n_qubits = 1
p = 0.15
density_matrix.load(mat)
circuit = QuantumCircuit(n_qubits)
circuit.add_gate(DepolarizingNoise(0, p))
circuit.update_quantum_state(density_matrix)
print(density_matrix)

 *** Density Matrix ***
 * Qubit Count : 1
 * Dimension   : 2
 * Density matrix :
(0.5,0) (0.4,0)
(0.4,0) (0.5,0)

[26]:

density_matrix.load(mat)
n_qubits = 1
p = 0.15
Parametric_circuit = ParametricQuantumCircuit(n_qubits)
Parametric_circuit.add_gate(DepolarizingNoise(0, 0.15))
Parametric_circuit.update_quantum_state(density_matrix)
print(density_matrix)

 *** Density Matrix ***
 * Qubit Count : 1
 * Dimension   : 2
 * Density matrix :
(0.5,0) (0.4,0)
(0.4,0) (0.5,0)

[ ]:

Qulacsでの混合状態

Contents